The major component in engineering is mathematics, it is instrumental as it is a great problem-solving tool. Although mathematics is broad certain categories in mathematics are used by engineers. Engineering mathematics is dominated by calculus. To understand calculus it is necessary to pay attention to details. In addition to learning calculus, there are other mathematical concepts that one needs to understand. These mathematical concepts include sets, numbers and functions. Additionally, there are special mathematical concepts engineering ought to consider such as trigonometric functions, as well as logarithmic and exponential functions. 

Set theory is closely interconnected to mathematical logic as these fields are instrumental in helping us understand the collection of objects and how they relate to each other before being introduced to engineering math equations. Why is set theory important? Set theory is important regarding engineering because it enriches engineering students with intuition in addition to enhancing their problem problem-solving skills therefore, it can solve comprehensive problems. Consequently, engineers as well as engineering students require an understanding of set theory principles and concepts involving mathematics.

Set Theory

Set is a building block in mathematics. In simple terms, a set is a collection of objects. In the case of an object, this includes numbers, functions, and other sets. The order of the objects within the set does not matter. 

• When there are finite numbers of objects within a set this is referred to as a finite set

• When there are infinite numbers within a set the set is referred to as an infinite set

Objects with a set are called members or elements. There are two basic ways that we can describe a set. 

1. Listing the Elements of a Set

A = {2,9,22} This set consists of three elements. The objects in the set are 2, 9, 22. Also, the order does not matter A = {2,9,22} is the same as A = {9,22,2}

It is also important to note that each element in the set can only appear once. Therefore, B = {4,6,4} is not a legal set, the second ‘4’ is perceived to be redundant and the appropriate set is written as B = {4,6}

At times it can be difficult to list all the elements, especially in a large set, therefore, we use ellipses but it is important to ensure that the pattern elements are clear. 

• Describing a set of the first 100 positive integers, the set can be described as {1,2,3 ……99, 100}

• Describing an infinite set can be described as {1,2,3 …}

2. Provide a Property that Precisely defines the elements of the set

Another way to describe a set is by providing the property of the set. 

1. All integers

B = {x| x is an integer} or B = {x: x is an integer} B comprises of all integers

2. Intervals of real numbers

 {x| x is real numbers and 2∠x≤3}: This represents a set of all real numbers that are greater than 2 and less than or equal to 3.

 The advantage is that this method can be used to describe a set event when we don’t know explicitly the elements of the set. An example is illustrated below

 { y | y is a real number and 2y4+y3+6y2+11+12=0}

This is valid, although at first glance the exact values of ‘y’ in the set are not known. If an object x is an element of s we write this x ∊ s. If x is not an element of s we write x ∉ s.

3. Special Sets

There are special sets

i. Empty set: Empty set denoted by symbol ∅. The empty set does not contain any elements at all. For instance:

 {x| x is real numbers and x2∠0 = ∅ }

NB: x ∉ ∅ for any x also an empty set is written as ∅ = { }

ii. Infinite set: If s is an infinite set we let #(s) denote the number of elements of s. We say #(s) is a cardinality of s. (or |s|). 

If s = {2, 4, 9, 11} then #(s) = 4

iii. Subset: A is a subset of B when every element of A can be found in B denoted as A ⊆ B. A proper subset is a set that is not equal to the larger set.

 A = {1,2,3}, 1 is an element of A and {1} is a subset of A.

In notation form  1 ∊ A and {1} ⊆ A

iv. Superset: B is a superset as it contains set A. However, it is important to note that a set that contains subset(s) is considered a Superset. 

Operations of Sets

Various operations can be performed on a set, these particular operations include addition and multiplication to get a new number the two primary operations on sets include:-

i) Union      ii) Intersection 

To better understand the set theory in certain instances it is vital to used venn diagrams. Consequently, set theory and Venn diagrams are closely linked. The Venn diagrams will be used to illustrate the union, intersection,

i) Union : 

A ∪ B of two sets A and B is the set of all objects that are elements of the A or of B.

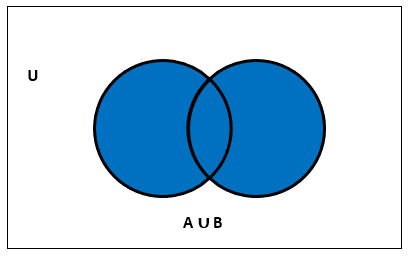
Formally written as  A ∪ B  = {x | x ∈ A or x ∈ B}

• Example:  {2, 3, 8} ∪ {1, 7, 11, 13} = {1, 2, 3,  7, 8, 11, 13}

 ii) Intersection :

A ∩ B of two sets A and B is a set of all objects that are elements of both A and B.

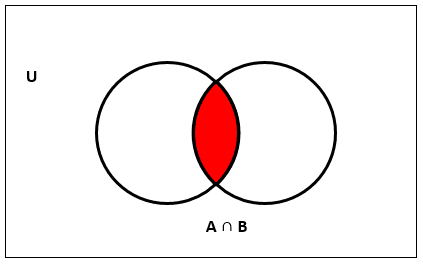
Formally written as  A ∩ B  = {x | x ∈ A and x ∈ B}

• Example:-

 {3, 5, 9, 11} ∩  { 5, 8, 11, 13} =  {5, 11}

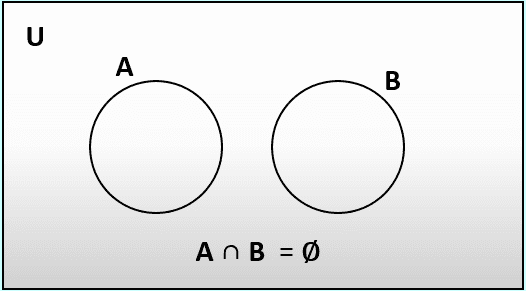
iii) Disjoint :

An instance where two sets do not have elements in common is referred to as a disjoint.

 If A ∩ B  = ∅  in this case we say that A and B are disjoint.

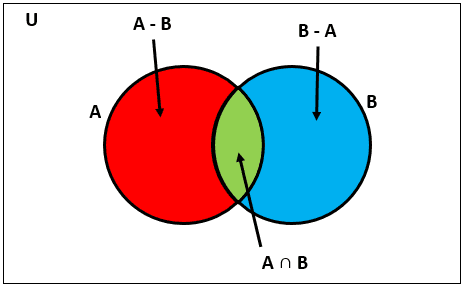
iv) Difference of sets :  

In regards to the difference between the two sets A and B 

A∖B = { x ∈ A | x ∉ B} This means that A∖B comprises all elements of A that are not in B

For example if A = {1,2} and A = {2,3} then   A∖B = {1} because 1 ∈ A and 1 ∉ B and 1 is the only element with this property. Similarly, B∖A =  {3} 

Set theory is a rich subject however, the description provided above barely scratched the surface.