The mathematical functions have a fundamental significance in the mathematical mode of thinking. Mathematics provides crucial modes for structuring and organizing knowledge, particularly when applied to technology thus enabling the engineers to develop reproducible, systematic, and transmittable information. 

Functions are mathematical tools whose objective is to associate input with a unique output: 

f(x) = 3x – 5

For any given input x ∈ ℝ, outputs the real number 3x – 5

Function f from a set A to a set B denoted f: A → B associates a ∈ ℝ an element f(a) ∈ B. The set A  is called the domain of f and the set B is called the codomain of f. We let Dom (f) denote the domain of f and Cod(f) denote the codomain of f.

Put simply:

A domain is what can go into a function that is, the possible inputs. Codomain refers to what comes out as the output of a function including the possible outputs. 

DOMAIN

In calculus, a function will almost always be ℝ. Also, one can assume that a function has a codomain ℝ unless otherwise specified, these functions are referred to as real-valued.

If the domain is not specified explicitly it is understood that a function has as its domain the largest subset ℝ of for which the function definition makes sense. 

Example :  f(x) = √(x)  has  domain  [ 0, +∞]  

Since in ℝ, we cannot take the square root of a negative number. Another point to make is f(x) = √(x)    even though the codomain of this function is ℝ.

RANGE

The function only actually outputs values that are nonnegative real numbers that is; f(x) ≥ 0  for all x ∈ Dom(f) to indicate that we say that the range  [ 0, +∞]. The range of a real-valued function f, denoted Rng(f) is the set of values that f outputs; that is Rng(f) = { y ∈ B | y = f(x) for some x ∈ Dom (f)} = { f(x) | x ∈ Dom (f)}.

Example 1: Find the domain and range of the function:  f(x) =1/√(x2-1)

There are two conditions on the domain f. As we can only take the square root of a non-negative number, we must have  x2-1 ≥ 0. But, we also cannot have a denominator equal to zero so we have x2>1 so x>1 or x< -1 thus domain is in [-∞, -1] ∪ [ 1, +∞]. As the denominator can be any positive real number the range [ 0, +∞]

We can perform operations on real-valued functions: We can add two functions f and g: 

(f+g)(x) = f(x)+g(x)

Note: This is valid at x where both f and g are defined so;

Dom(f+g) = Dom(f) ∩ Dom(g)

Similarly: We can subtract, multiply and divide.

(f-g)(x) = f(x)-g(x)

(fg)(x) = f(x)g(x)

(f/g)(x) = f(x)/g(x)

All of these have  the same domain as (f + g), with the exception of (f/g) that has added restriction that g(x) ≠ 0

We can multiply a function f by C ∈ ℝ;  (Cf)(x) =C. f(x) It is clear that Dom(cf) = Dom(f)  

We can compose two functions: 

(fog)(x) = f(g(x))

Note that for  (fog)(x) to be defined we must have x ∈ Dom(g) and g(x)  ∈ Dom(f). Also, notice that the order of the functions is important  fog is in general not the same as gof

Let f be a real-valued function, a real-valued function called g is called the inverse  of f if 

(f(g(x)) = x for  all  x ∈ Dom (g) and (g(f(x)) = x for  all x ∈ Dom (f)

We denote this by g=f -1

Notice that if g is an inverse of f then f is also an inverse of g by the symmetry of the definition.  Further since f and g essentially “undo” each other, the result of the next problem should make sense. 

Example 2: Show that if g is an inverse of f, then Dom(f) = Rng(g) and Dom(g) = Rng(f)

Solution : 

(g(f(x)) = x for  all  x ∈ Dom (f) we see that   x ∈ Dom (f) implies that   x ∈ Rng (g). So Dom (f) ⊆ Rng (g), on the other hand if  y ∈ Rng (g) then y =g(x)

 For some   x ∈ Dom (g) and thus  f(y) = f(g(x)) = x

In particular,  y ∈ Dom (f) so Rng (g) ⊆ Dom (f) combining these two subsets inclusion gives us Dom (f) = Rng (g). By the symmetry of the definition of inverse, we also have that f is an inverse of g and thus the previous argument shows that  Dom (g) = Rng (f) 

The next example illustrates we can refer to ‘the’ inverse of f rather than the ‘an’ inverse of f.

Example 2: Show that if f-1 exists then it is unique; that is, show that if g and h are both inverses of  f, the g = h

Solution: 

We know that  Dom (g) = Rng (f) =Dom (h) let x be an element in the shared domain of g and h; we will show that g(x) = h(x) since   x ∈ Rng (f) there is some y ∈ Dom (f) such that f(y) =x

But then:

g(x) =g( f(y))=y=h(f(y) = h(x) so g(x) = h(x) for all x in their (shared) domain and thus the functions are equal. 

Let f, be a function and A ⊆ Dom (f) the image of A under f denoted f(A) is 

f(A) ={  y ∈ Cod (f) | y =f(x) for some x ∈ A }  Let B ⊆ Cod (f). The preimage of B under f, denoted f -1(B) is: 

f -1(B) = {  y ∈ Dom (f) | f(x) ∈ B }

Informally, the image of A is the set where A “gets sent to” and the preimage of B is the set “that gets sent to B”. 

Notice that, by definition f (Dom (g))= Rng (f) and f -1 (Rng (f)) = Dom (f)

NOTE: f -1 has two different but related meanings. If f has an inverse and x ∈ Rng(f) then f -1(x) inverse function of f. On the other hand, if B ⊆ Cod (f), the f -1(B) denotes the preimage of B under f. We don’t require that f have an inverse to define f -1(B) in the former x is a number B is a subset.

GRAPH FUNCTIONS 

Graphs allow for math functions visualization that gives an intuitive understanding of the existing problem to have a better problem-solving intervention. The picture illustrates a graph f(x) = x² + 2x – 3. When investigating geometric properties of graphs; Functions play a crucial role in calculus.

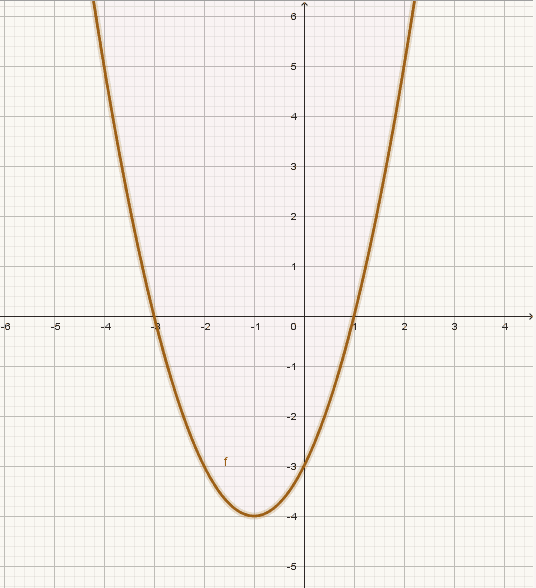
Graphs are constructed on the Cartesian plane shown in the picture above. The cartesian plane is the set of all ordered pairs of real numbers in order words it is: {(x, y) | y ∈ ℝ } This is often denoted as ℝ×ℝ or ℝ2

NOTE: Point (x, y) is in the graph of a function f(x)  and only if y = f(x). The graph of f is the of all points (x, f(x)) where x ∈ Dom (f) 

FORMAL DEFINITION OF A GRAPH : 

The graph of the real-valued function f is the set {(x, f(x)) | x ∈ Dom (f)}. Graphing a mathematical function uses a cartesian plane to display input-output pairs to generate a visual representation of the information to make the relationship easier to understand. 

FUNDAMENTAL PROPERTY OF GRAPHS OF FUNCTIONS 

Example a): Let f be a function. Explain why every vertical line in the plane intersects the graph of f at most one point. 

Solution: 

For any x ∈ ℝ, the vertical line x = a in the plane is the subset { (a, y) | x ∈ ℝ}. There is at most one point in the graph f with first coordinate a and that is the point (a, f(a)) if a ∈ Dom (f).

If a ∉ Dom (f) there is no point in the graph of f with the first coordinate a and hence the line x = a does not intersect the graph of f at all.

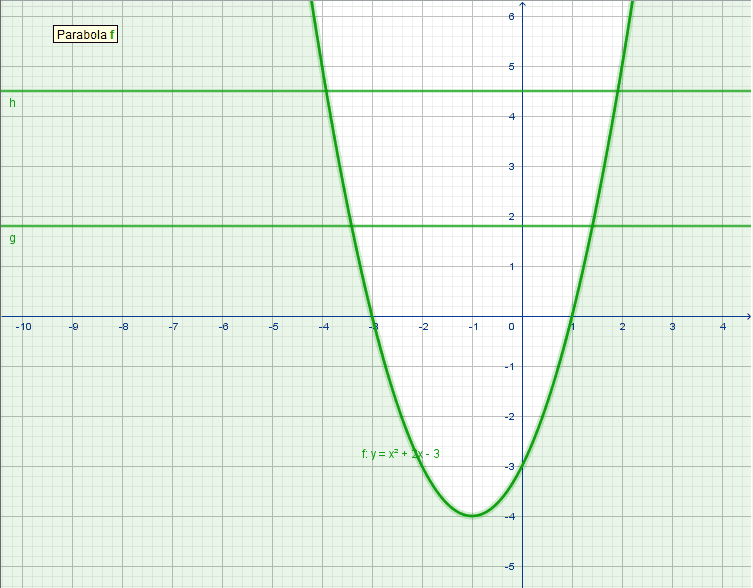
For any function f any vertical line (that is any governed by x=a for some a ∈ ℝ) must intersect the graph of f at most 1 point. Conversely, if there is a subset S of the cartesian plane for which there is some vertical line x=a that intersects S in more than 1 point, the S cannot be the graph of a function. 

The intuition of the converse portion of the vertical line test should be clear. If some line x=a intersects S in two distinct points (a,b) and (a,c) then there’s no way S could be the graph of a function f  since we’d need f(a) = b and f(a) = c but f(a) can only equal one number.

There’s no such restriction about horizontal lines. For example, looking back at our parabola   y = x² – 2x – 3. (below)

There are a lot of horizontal line intersections that graph in at most one point and have a very special property. 

Example: Let f be a function and suppose that every horizontal line y=b intersects the graph of f at most one point. Show that  f has an inverse f-1

Solution:

Suppose the line y=b intersects the graph of f at (a,b).  We know that b=f(a) by definition since it lies on the graph of f, so our inverse for f will have to map b back to a. This tells us how to define the inverse.

Define a function g as follows: If the line y=b intersects the graph of  f at the point (a,b)  the g(b)=a

NOTE

Dom (g) = Rng (f) Since any such horizontal line will intersect the graph in at most one point the function g is well-defined. By construction, we have g(f(a))=a for any a ∈ Dom(f). Furthermore, if b ∈ Dom(g) then the line y=b intersects the graph of f at some point (a,b), so f(g(b))=f(a)= b thus g =f-1

Source:

Patrick, David. The Art of Problem Solving – Calculus. Aops Incorporated, 15 Apr. 2013.